I worked on this challenge with @dariosharp.
This crypto challenge (https://giant-goannas.ctfcompetition.com/) has a quite easy request
So we have to choose the right number n-times consecutively. If we make a mistake, we have to repeat this process from the beginning (obviously with different numbers). In the comment of the previous web page of the challenge we find this code
class SecurePrng(object):
def __init__(self):
# generate seed with 64 bits of entropy
self.p = 4646704883L
self.x = random.randint(0, self.p)
self.y = random.randint(0, self.p)
def next(self):
self.x = (2 * self.x + 3) % self.p
self.y = (3 * self.y + 9) % self.p
return (self.x ^ self.y)
So let’s do some math
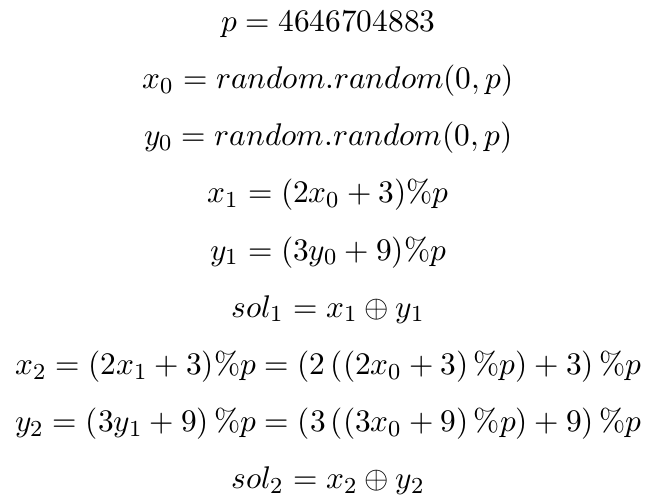
so assume that we know the first two correct number (just guess that): we only have to solve this system of equations in order to find the first two random integer
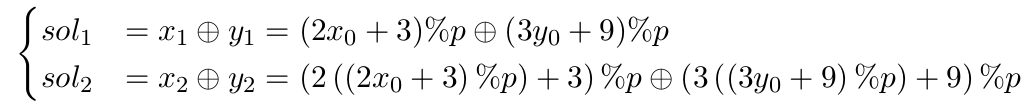
We guess the fist two step (not so difficult, it happens with 0.25 probability): in our case
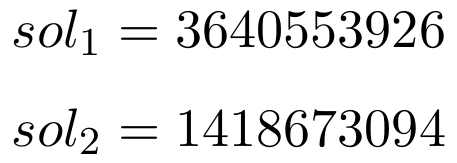
Mathematica refuses to solve that equation system: no problem, let’s use z3!
from z3 import *
import sys
s1cor = int(sys.argv[1])
s2cor = int(sys.argv[2])
dimVector =35
x = BitVec('x', dimVector)
y = BitVec('y', dimVector)
p = BitVec('p',dimVector)
s1 = BitVec('s1',dimVector)
s2 = BitVec('s2',dimVector)
s = Solver()
s.add(p == 4646704883L)
s.add(s1 == s1cor)
s.add(s2== s2cor)
s.add( ( ( ( 2 * x + 3 ) % p ) ^ ( ( 3 * y + 9 ) % p ) )==s1)
s.add(( ( ( 2 * ( ( 2 * x + 3 ) % p ) + 3 ) % p ) ^ ( ( 3 * ( ( 3 * y + 9 ) % p) + 9 ) % p ) )==s2)
while s.check() == sat:
class SecurePrng(object):
def __init__(self,x,y):
self.p = 4646704883L
self.x = x
self.y = y
def next(self):
self.x = (2 * self.x + 3) % self.p
self.y = (3 * self.y + 9) % self.p
return (self.x ^ self.y)
def getX(self):
return self.x
def getY(self):
return self.y
m = s.model()
pMy = 4646704883L
myObj = SecurePrng(int(str(m[x]))%pMy,int(str(m[y]))%pMy)
mySol1 = myObj.next()
mySol2 = myObj.next()
if mySol1 == s1cor and mySol2 == s2cor and int(str(m[x]))<= pMy and int(str(m[y])) <= pMy :
print "x = " + str(m[x]) + " ; y = " + str(m[y])
s.add(Or(x != s.model()[x], y != s.model()[y]))
just few notes: there are more than one solution of that system, so we check every solution that z3 proposes.
Run that s**t!
$ time python solver.py 3640553926 1418673094
x = 3714993585 ; y = 2248563082
real 0m0.591s
user 0m0.556s
sys 0m0.012s
ok: we found the two random seed and and we were able to generate all the solution.
>>> import random
>>>
>>> class SecurePrng(object):
... def __init__(self):
... self.i = 0
... self.p = 4646704883L
... self.x = 3714993585 % self.p
... self.y = 2248563082 % self.p
... def next(self):
... print self.i
... self.i += 1
... self.x = (2 * self.x + 3) % self.p
... self.y = (3 * self.y + 9) % self.p
... return (self.x ^ self.y)
... def getX(self):
... return self.x
... def getY(self):
... return self.y
...
>>>
>>> mySol = SecurePrng()
>>> print "x0 = " + str(mySol.getX())
x0 = 3714993585
>>> print "y0 = " + str(mySol.getY())
y0 = 2248563082
>>> print mySol.next()
0
3640553926
>>> print "x1 = " + str(mySol.getX())
x1 = 2783282290
>>> print "y1 = " + str(mySol.getY())
y1 = 2098984372
>>> print mySol.next()
1
1418673094
>>> print mySol.next()
2
2142807111
>>> print mySol.next()
3
3977384148
...
...
>>> print mySol.next()
100
31332507
After 100 step we get the flag CTF{!_aRe_y0U_tH3_NSA:-?!}
Solver for this challenge can be found here.
